O biólogo profissional e matemático amador Aubrey de Grey surpreendeu o mundo da matemática ao resolver parcialmente um enigma de longa data.
O enigma, conhecido por problema Hadwiger-Nelson, surgiu quando Edward Nelson e Hugo Hadwiger se questionaram sobre o menor número de cores necessário para colorir todos os pontos de um gráfico, sem que dois pontos surgissem unidos e pintados da mesma cor.
Ou seja: imagine que tem um gráfico, um grupo de pontos ligados por linhas. Essas linhas têm o mesmo comprimento e tudo está dentro do mesmo plano. Se tivesse que colorir todos os pontos de forma a que dois pontos ligados não tivessem a mesma cor, qual seria o menor número de cores que iria precisar?
Simplificando, a pergunta que permanecia sem resposta era: se cada um desses pontos (ou vértices) fossem coloridos, de quantas cores diferentes iríamos precisar para que dois pontos unidos não compartilhassem a mesma cor?
A pergunta é tão simples quanto o problema de Hadwiger-Nelson, mas resolver o enigma não é uma tarefa nada fácil – especialmente quando a questão contempla teoricamente um número infinito de vértices.
Formulado de forma abrangente pelo matemático Edward Nelson, em 1950, o problema nunca foi definitivamente resolvido, mas não por falta de tentativa. Logo após a primeira pergunta, os matemáticos descobriram que exigiria não menos do que quatro cores, mas não precisaria de mais do que sete.
Durante décadas, houve um progresso mínimo na tentativa de diminuir essa margem, até este mês – quando De Grey enviou sua nova solução para o arXiv.org. Mas o amador, que só recorre à matemática no tempo livre e por diversão, não é apenas conhecido pela mais recente solução.
De Grey é conhecido por ser um estudioso da longevidade, que sustenta que os processos de envelhecimento humano podem realmente ser revertidos. Além disso, lidera uma fundação de pesquisa que se dedica a investigar como a medicina regenerativa pode curar “doenças relacionadas à idade”.
Foi durante suas férias de Natal que Aubrey De Grey conseguiu se dedicar um pouco mais à matemática e colocar de lado a suposição que os matemáticos haviam feito (e em que tinham acreditado) durante décadas.
(dr) De Grey

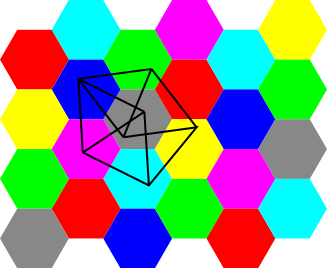
Gráfico com 1.581 vértices de De Grey
De Grey demonstrou que um gráfico com 1.581 vértices requer, pelo menos, cinco cores diferentes – e não quatro, como se pensava até então. Mas como o amador conseguiu chegar a essa solução?
O biólogo e matemático “brincou” com o gráfico de Moser, composto por sete vértices e onze linhas, e chegou à conclusão de que um compósito de 20.425 pontos exigia mais do que quatro cores.
Assim, De Grey simplificou seu gráfico de cinco cores para 1.581 vértices e, compartilhando o seu trabalho, convidou outros matemáticos a se juntarem na difícil resolução para encontrar gráficos com menos pontos, que requerem pelo menos cinco cores.
Foram vários os matemáticos que participaram no desafio. Atualmente, o novo registro parece ser de 826 vértices. No entanto, como há um grande interesse pelo problema de Hadwiger-Nelson e pelas cores que não podem se tocar, não há como saber que rumo irá tomar a resolução do enigma.
Por sua vez, De Grey, o estudioso que pensa que irá viver até os mil anos, é bastante humilde em relação à sua contribuição. “Tive uma sorte extraordinária”, disse.
Ciberia // ZAP