Sabemos há muito tempo que Saturno é cheio de anéis, mas as partículas dentro deles, que se empurram e colidem, eram um mistério.
Viajando a uma velocidade vertiginosa, todos os choques e tamanhos dessas partículas pareciam aleatórios e casuais. Agora, uma nova teoria matemática traz ordem ao caos.
Um grupo de físicos, matemáticos e astrônomos explicou como a distribuição de tamanho das diferentes partículas, que vão desde centímetros a dez metros, segue uma relação muito simples.
A teoria não só esclarece a estabilidade dos anéis de Saturno, como pode revelar mais sobre as idades e condições de outros planetas e asteroides que também possuem anéis.
Ordenado
Saturno é cercado por anéis imensos construídos de pedaços de água congelada, com uma pitada de material rochoso. Os anéis podem atingir uma largura de 300 mil quilômetros, e as partículas podem viajar a milhares de quilômetros por hora.
NASA

De longe, os anéis de Saturno parecem uma coisa sólida, homogênea e contínua.
Os pesquisadores descobriram que as partículas dos anéis são soltas e porosas. Quando duas partículas se chocam, se estiverem se movendo lentamente o suficiente, irão se fundir em uma só. Mas, se estiverem se movendo muito rapidamente, vão se destroçar.
O novo modelo mostra matematicamente como este comportamento simples está de acordo com a distribuição estranhamente precisa de tamanhos de partículas nos anéis.
Regra de 3
Desde os anos 1980, os pesquisadores observam uma relação estrita nos tamanhos de partículas nos anéis de Saturno, que segue aproximadamente uma “lei do cubo inverso”.
Por exemplo, uma partícula de duas vezes maior do que a outra será oito vezes menos comum, e uma partícula três vezes maior será 27 vezes menos comum.
Os cientistas descobriram que a distribuição das partículas de acordo com seu tamanho também segue de forma semelhante esta regra de 3 (entre 2,75 e 3,5).
Sistema universal
A regra é ainda mais ampla do que os pesquisadores inicialmente pensaram: há apenas dois anos, eles descobriram que os asteroides têm anéis também. Chariklo e Chiron, por exemplo, seguem o modelo de Saturno.
Esses asteroides são muito menores do que o planeta, mas seus anéis não só são parecidos como têm distribuições similares de partículas, o que sugere que o modelo é bastante universal.
No entanto, ele pode não se aplicar a sistemas com um número excessivo de colisões ou com muito poucas colisões e, portanto, mais investigação observacional seria necessária para ver quais sistemas de anéis são contrários ao modelo.
Como anéis se formam
O modelo também pode ensinar mais aos pesquisadores sobre planetas e asteroides. “Agora sabemos como os anéis devem ser construídos. Suponha que descobrimos novos anéis, de algum planeta. Apenas pela medição da distribuição do tamanho das partículas no anel, podemos dizer se ele é jovem ou se já experimentou algum impacto catastrófico no passado. Se a distribuição segue a forma de cubo inverso, nada aconteceu nos últimos 10 mil anos”, disse Nikolai Brilliantov, matemático da Universidade de Leicester, na Inglaterra, e principal autor do estudo.
NASA
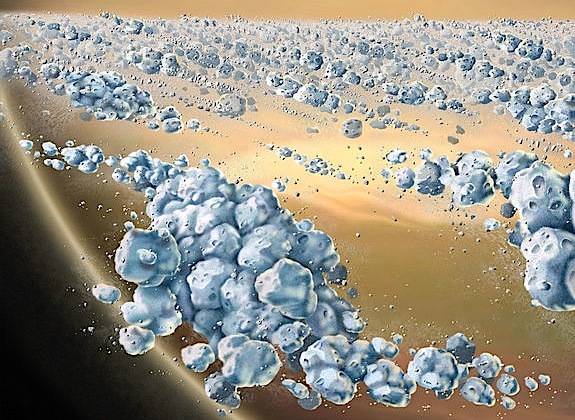
Concepção artística das partículas dentro dos anéis de Saturno
Além disso, ao olhar para o tamanho máximo das partículas, os pesquisadores podem ser capazes de aprender mais sobre as substâncias a partir das quais os anéis se formam.
Segundo Jeff Cuzzi, cientista interdisciplinar da missão Cassini que não esteve envolvido no estudo, o novo trabalho confirma pesquisas anteriores sobre como os anéis de Saturno se formam, e descreve-o em um sentido matemático mais geral.
“A conclusão geral até à data é que as partículas são soltas e não sólidas, e que as distribuições de tamanho que vemos não são primordiais, mas são altamente evoluídas por dinâmicas locais”, disse.
Mais anéis precisam ser estudados
Conforme o processo de medir anéis distantes for repetido em mais planetas e asteroides, a equipe vai ter mais e mais situações para alimentar o modelo.
Os anéis de Saturno chegaram a um estado estável, mas outros anéis no universo podem não ser tão bem estabelecidos: Brilliantov diz que o próximo passo é aprofundar como anéis evoluem com o tempo para chegar a um equilíbrio.
“Em nosso sistema solar, há uma abundância de anéis que não são explorados”, afirma. “Se tivermos informações suficientes, podemos aplicar uma teoria mais complicada, bonita e abrangente para esses sistemas”.